Binary Indexed Tree and Its Applications on LeetCode
Why Do We Need a Binary Indexed Tree?
Problem Setup
Question:
Given an integer array input = [1,2,7,4,3], how can we quickly calculate the sum of the first K numbers?
Solution:
A common approach is to build a prefix sum array preSumArray, where preSumArray[i] represents the sum of the first i elements.
With this, the sum of the first N numbers can be retrieved in O(1) time. If we need to perform K queries, the total complexity is O(K).
Making It Harder
Question:
Now suppose we still want to query prefix sums on the same array input = [1,2,7,4,3], but before querying we might increase or decrease the value at index i.
Solution:
If we continue to rely on preSumArray, then every update at position i requires modifying all subsequent entries of the array.
That means each update costs O(N), and K queries with updates would cost O(KN).
If we abandon preSumArray, updates are O(1), but each query would degrade to O(N).
This is where a Binary Indexed Tree (Fenwick Tree) helps us balance both operations efficiently.
Prerequisite: A Binary Trick
A useful bitwise operation in this context is:
1 | lowbit(x) = x & (-x) |
This extracts the largest power of 2 that divides x, i.e., the value of the rightmost 1 bit.
Examples:
5 & -5 = 110 & -10 = 212 & -12 = 4
Binary Indexed Tree (Fenwick Tree)
Definition
Conceptually, it’s still an array—similar to a prefix sum array—but instead of storing complete prefix sums, it stores the sum of the last lowbit(i) elements up to index i.
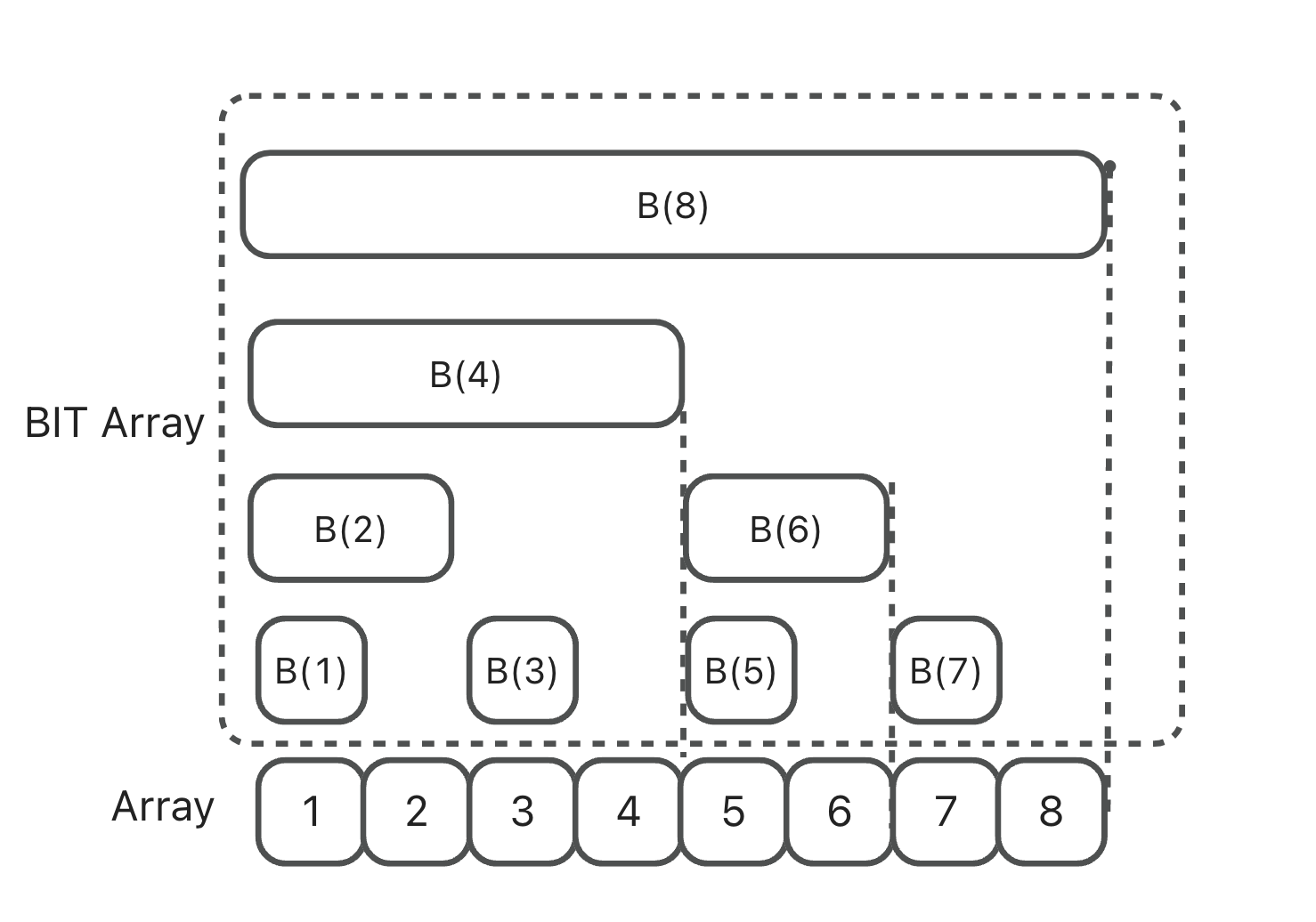
1 | B(1) = A(1); |
Note: The index of a Binary Indexed Tree must start from 1.
Core Operations
The Binary Indexed Tree mainly supports two operations: prefix sum queries and updates.
Querying Prefix Sums
Example:
1 | getSum(7) = A(1)+...+A(7) = B(4)+B(6)+B(7) |
Implementation:
1 | public int getSum(int x) { |
Recursive form:
1 | public int getSum(int x) { |
Time complexity: O(log N)
For a range sum sum(i, j), simply compute getSum(j) - getSum(i-1).
Updating Values
Example: update(6, 7) means adding 7 to position 6. This requires updating B(6) and B(8).
Implementation:
1 | public void update(int x, int value) { |
Applications on LeetCode
LeetCode 493 — Reverse Pairs
Question:
Given an array nums, a pair (i, j) is called a reverse pair if i < j and nums[i] > 2*nums[j].
Return the total number of reverse pairs.
Example Input:
1 | [1,3,2,3,1] |
Output:
1 | 2 |
Solution:
We can transform the problem into:
For each
j, count how many elements to its left are greater than2 * nums[j].
Steps:
- Sort and discretize the array into a mapped range
1..n. - Count occurrences of each number.
- Use a BIT to query prefix sums over the mapped values.
Code:
1 | class Solution { |
Similar Problems
- LeetCode 307 — Range Sum Query – Mutable
- …and many others that require efficient prefix sums with updates.