Ray‘s Blog
0%

KMP algorithm

Posted on In Valine:

KMP:

​ The KMP (Knuth-Morris-Pratt) algorithm is an algorithm for string search that finds the occurrence of a word W within a text string S.

The basic idea is that when a substring does not match the target string, it is known enough information to be able to determine that the next search step will not result in a missed check of the target string. In this way, the algorithm does not perform an invalid check.

The following are the steps of the KMP algorithm:

  1. Construct a “partial match table” (also called a “failure function”). This is an array, and for a given lookup word, each element of the table contains the position where the lookup word should jump when the match fails.
  2. Use this table to perform string searches. When a match failure occurs in a text string, you can skip directly to the previous part that is known not to match.

Why KMP

​ In the first approach, if the comparison from String[i] fails, the algorithm directly starts trying to compare from S[i+1]. This kind of behavior is a typical “not learning from previous mistakes”.We should note that a failed match will provide us with valuable information - if the match between String[i : i+len(P)] and P fails at the r th position, then from S[i] : the first (r-1) consecutive characters must be exactly the same as the first (r-1) characters of P

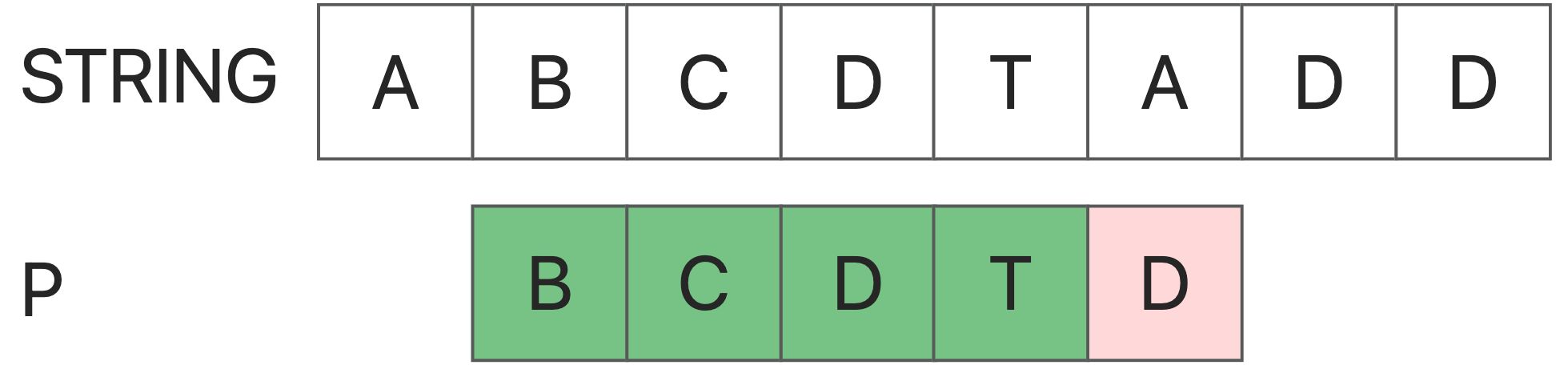
​ Therefore, we can skip those unlikely strings as much as possible to optimize our method。

Give a Exapmle:

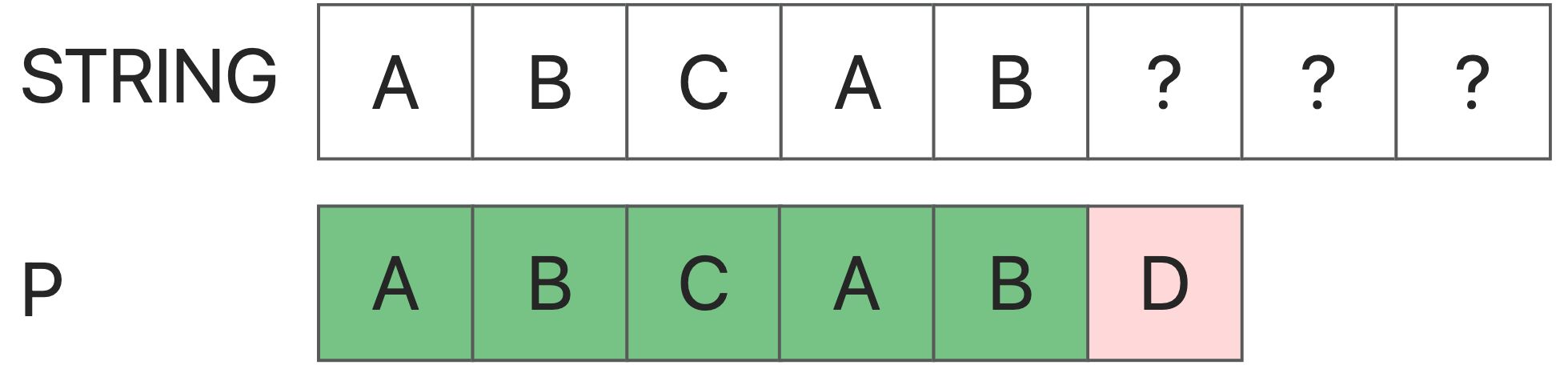
​ First, P[5] fails to match, then it means that S[0:5] is equal to P[0:5], which is “abcab”.

Now let’s consider: from S[1], S[2], S[3] Is there any chance that the initial matching attempt will succeed?

When we start in S[1], it won’t success. Because we can see : P[1] != P[0], But P[1] = S[1], So P[0] != S[1].

As same in S[2].

But when we start in S3: P[0] = P[3], S[3] = P[3], so P[0] = S[3].

We can find that in S[3], it is possible to match successfully. And we will find that if it is known that S and P are the same within the length L, then whether any i can be used as the starting point of matching depends only on whether P[0] = P[i] are equal. Here we can get the core next array of the KMP algorithm

Next Array

The next array is for the pattern string. The next array of P is defined as: next[i] represents a substring of P[0] ~ P[i], so that the first k characters are exactly equal to the largest k of the last k characters. In particular, k cannot be i+ 1 (Because this substring has only i+1 characters in total, it must be equal to itself, so it is meaningless). In fact, it is to get the maximum length of the longest same prefix and suffix in the P string when different starting points i.

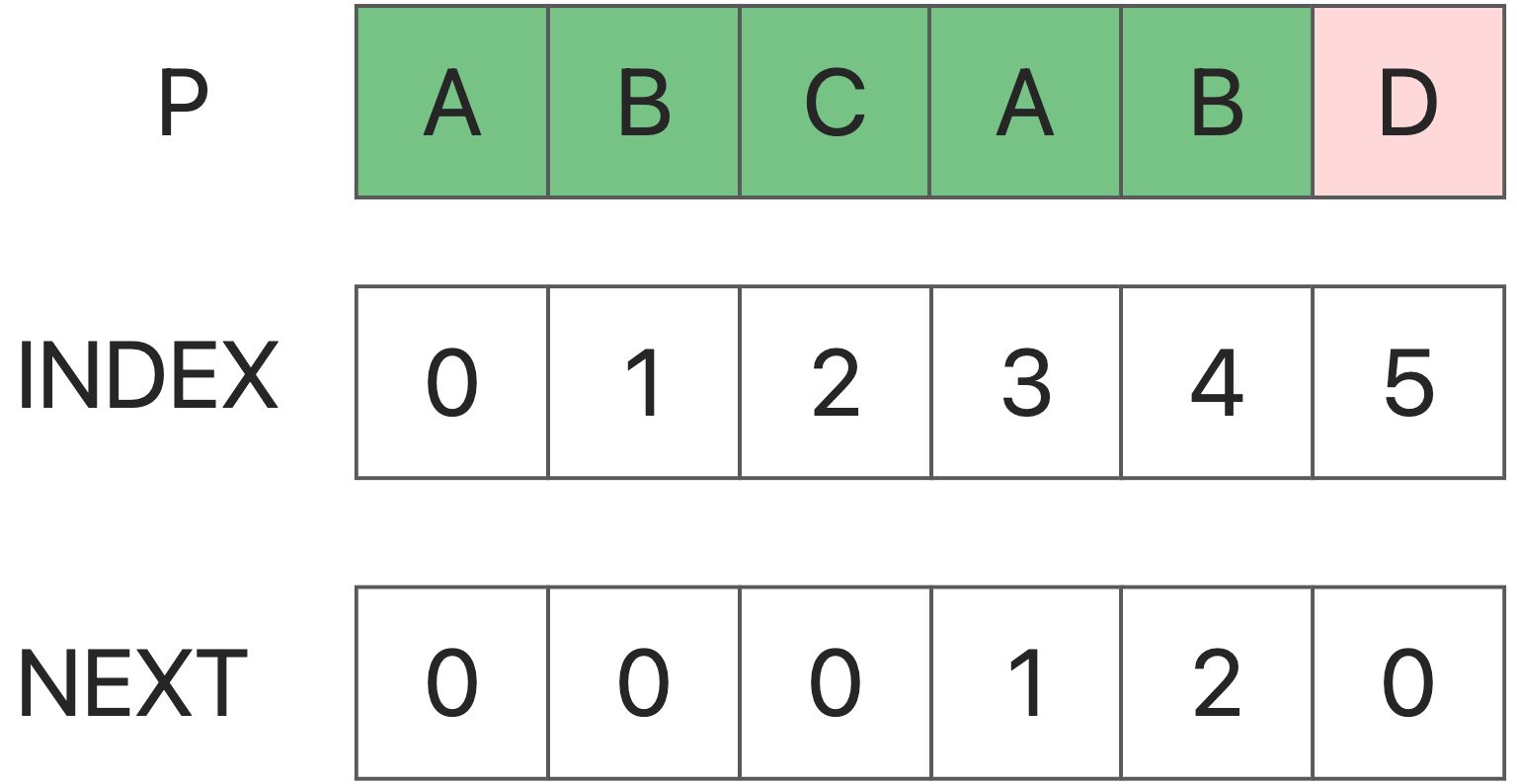
NOW, How to use next array match

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int i=0;
int j = 0;
getNext(needle,next);
while (i < length && j < length1)
{
    if (j == -1 || haystack.charAt(i) == needle.charAt(j))
    {
        i++;
        j++;
    }
    else {
        j = next[j];
    }
}

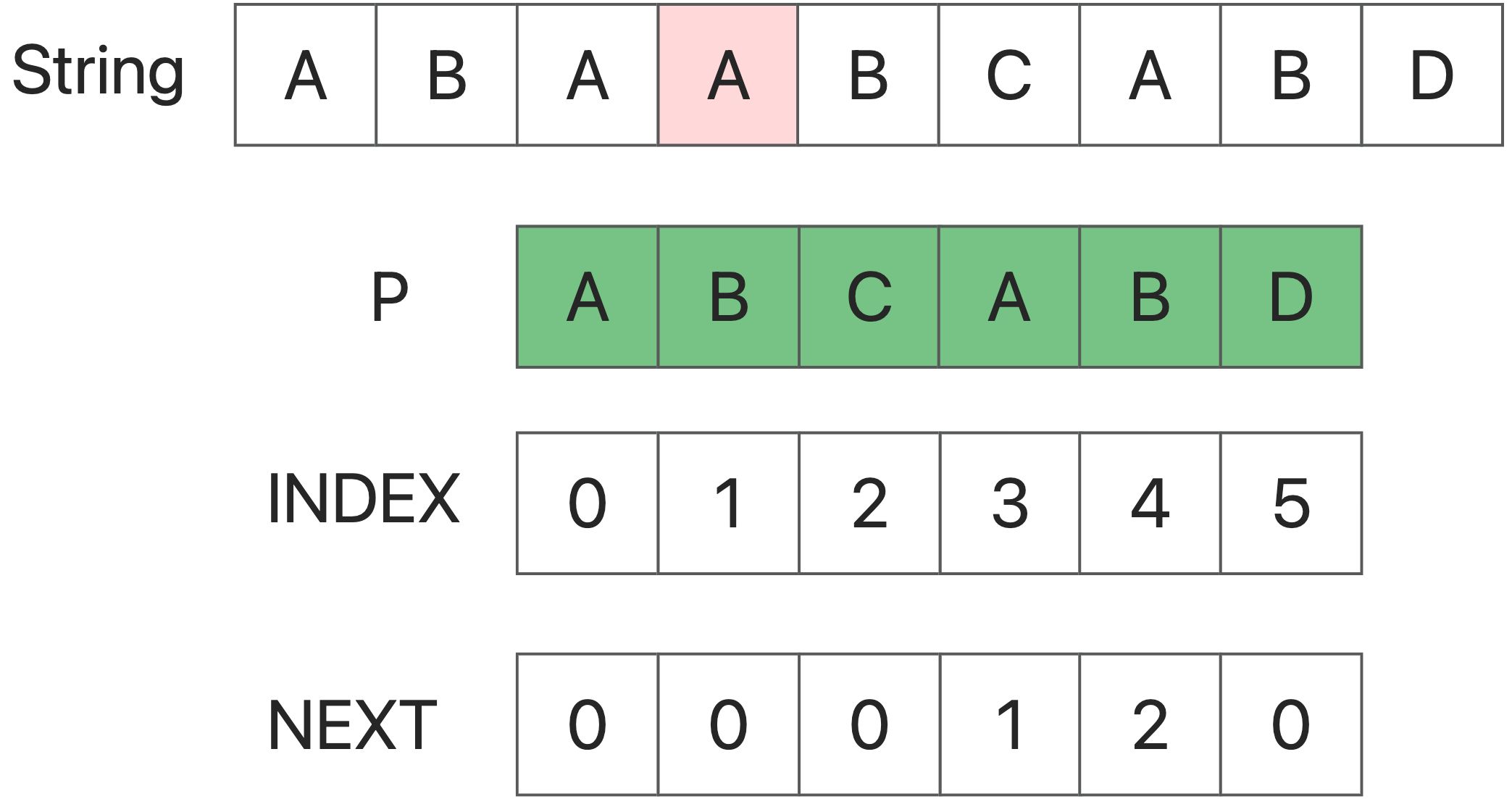
First: we use two point to mactch the Strings. The problem is how to change the point?

Second:

String[i] != P [j] ,now we need change the j to find a new start which prefix of String is equals to P. Only in this way it may success. So, next array is useful: j = next[j]

How to get next array

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void getNext(String p, int [] next)
    {
        next[0] = -1;
        int i = 0, j = -1;

        while (i < (p.length())){
            if (j == -1 || p.charAt(i)==p.charAt(j)) {
                ++i;
                ++j;
                next[i] = j;
            }
            else {
                j = next[j];
            }
        }
    }

this code use a small skills：make next[0] = -1 . you can remember it ,it will make easier to code;

dynamic programming:

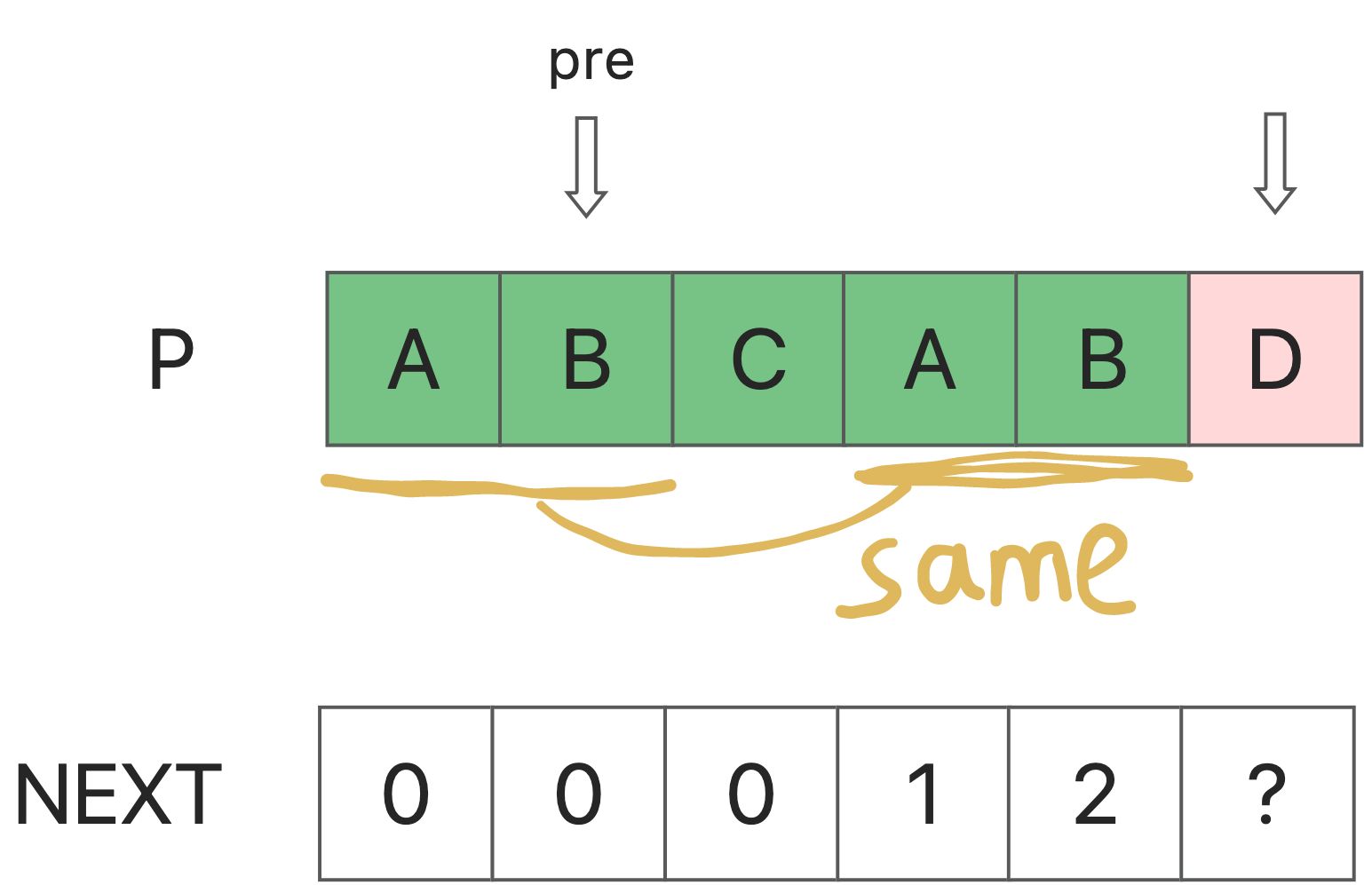
next[i] means the max(i) that p[0,next[i]] = p[i-next[i],i]

so, for if we know next[0],next[1],…next[i-1], how to know next[i]?

set next[i-1] = pre

ifp[i] = p[pre+1] , it means next[i] = pre+1

else if p[i] != p[pre+1], it means p[i-pre-1,i-1] = p[pre-1]

we should reduce the pre. pre = next[pre]

Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/**
     * now we can use kmp algorithm，a prefix matching algorithm
     *
     */

    public int strStr(String haystack, String needle){
        //in first method,we can find that we need match all the substring if it's not match.
        //some message have been lost: the prefix of the last string we have compared.
        //we can start with the same prefix string to match,so that the time can be saved
        // we can store the same prefix in a array or list, so we called kmp algorithm
        int length = haystack.length();
        int length1 = needle.length();
        int i=0;
        int j = 0;
        int [] next = new int [length1];
        getNext(needle,next);
        while (i < length && j < length1)
        {
            if (j == -1 || haystack.charAt(i) == needle.charAt(j))
            {
                i++;
                j++;
            }
            else {
                j = next[j];
            }
        }

        if (j == length1){
            return i - j;
        }
        else {
            return -1;
        }
    }

    void getNext(String p, int [] next)
    {
        next[0] = -1;
        int i = 0, j = -1;

        while (i < (p.length())){
            if (j == -1 || p.charAt(i)==p.charAt(j)) {
                ++i;
                ++j;
                next[i] = j;
            }
            else {
                j = next[j];
            }
        }
    }