树状数组与力扣中的应用
为什么会需要树状数组
思考以下问题
QA:
假设存在一个整数序列 input,例如 intput = [1,2,7,4,3],要求前 K 个数的和。
Solution:
一般我们会求一个前缀和数组 preSumArray,其中 preSumArray[i] 代表前 i 个数的和。
这样我们求前 N 个数的和只需要返回 preSumArray[N],时间复杂度为 O(1)。如果需要查询 K 次,则复杂度为 O(K)。
升级这个问题
QA:
假设存在一个整数序列 input,例如 intput = [1,2,7,4,3],现在在我们获取前 N 个数的和时,可能会先将 i 位置的数增加/减少 value。
Solution:
一般我们会求一个前缀和数组 preSumArray,其中 preSumArray[i] 代表前 i 个数的和。
但是如果我们需要在第 i 位置插入一个数 x,在进行更新时需要更新 i 之后的所有 preSumArray。
此时单次的更新时间为 O(N),K 次查询的复杂度为 O(KN)。
如果我们不使用 preSumArray,那么更新复杂度为 O(1),查询复杂度会变为 O(N)。
这时树状数组可以帮助我们快速解决这个问题
前置知识——二进制的应用
二进制有很多有趣的应用,这里介绍一个用法:
1 | lowbit(x) = x & (-x) |
这个式子的目的是 求出能整除 x 的最大 2 次幂,也就是 x 最右边的 1。
例子:
5 & -5 = 110 & -10 = 212 & -12 = 4
树状数组(Binary Indexed Tree, BIT)
定义
本质上它仍是一个数组,与 preSumArray 相似,存的依旧是和数组,但是它存放的是 i 位之前 (包括 i),lowbit(i) 个整数的和。
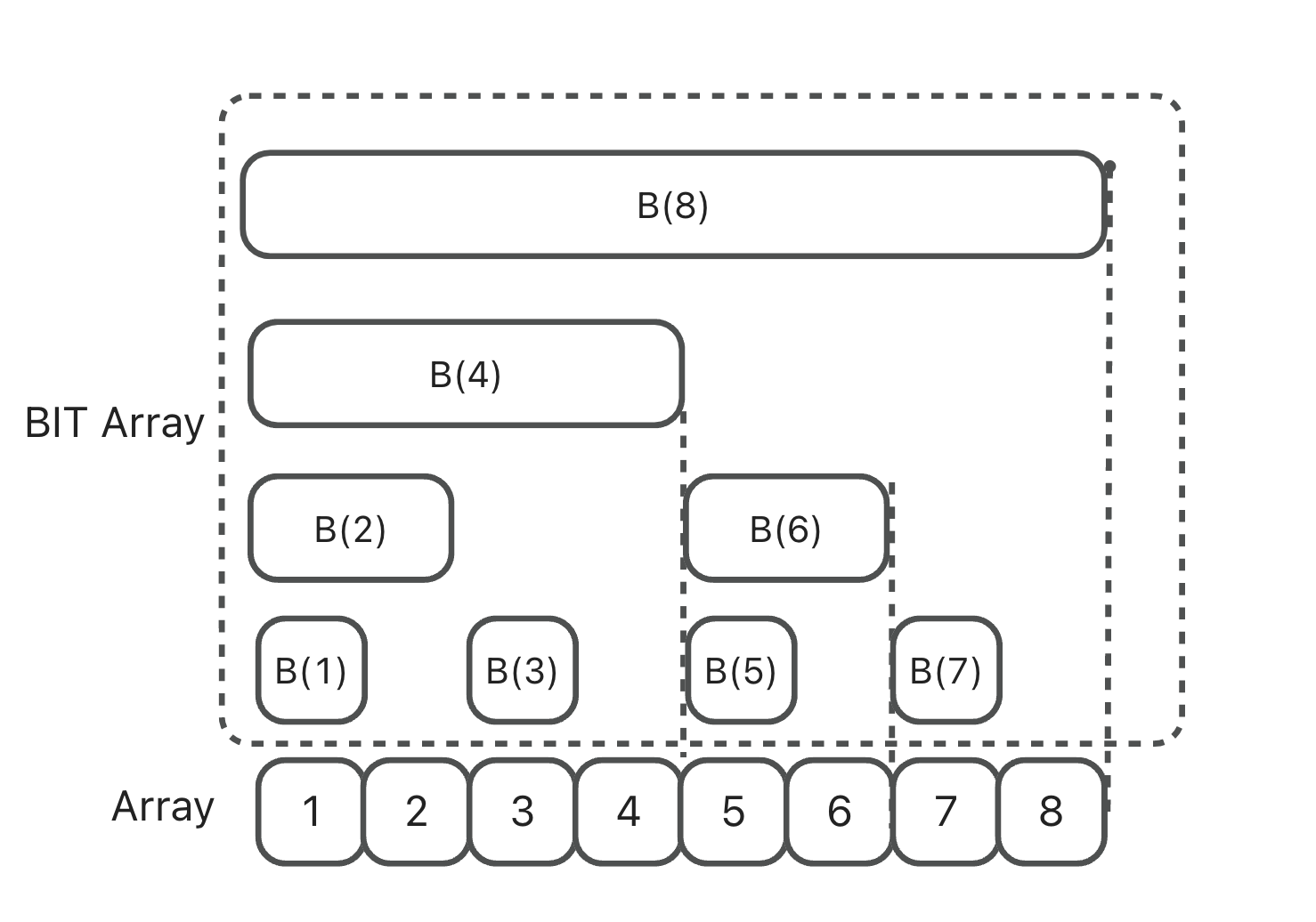
1 | B(1) = A(1); |
tip: 树状数组的下标必须从 1 开始
使用
树状数组主要解决两个操作:求和 与 更新。
求和
例子:
1 | getSum(7) = A(1)+...+A(7) = B(4)+B(6)+B(7) |
实现代码:
1 | public int getSum(int x) { |
递归形式:
1 | public int getSum(int x) { |
复杂度:O(logN)
如果要求 sum(i,j),只需要 getSum(j) - getSum(i-1)。
更新
例子:update(6,7),即在位置 6 加上 7,需要更新 B(6) 和 B(8)。
实现代码:
1 | public void update(int x, int value) { |
力扣中的应用
LeetCode-493
QA:
给定一个数组 nums ,如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个 重要翻转对。
返回给定数组中的重要翻转对的数量。
Input:
1 | 输入: [1,3,2,3,1] |
Solution:
题目可以转换为求 在 j 元素左边比它 2 倍大的元素有几个,并求和。
- 将数组排序并离散化映射为 1-n 的有序序列。
- 统计每个数的出现次数。
- 求前缀和,得到映射后的个数。
Code:
1 | class Solution { |
类似问题
- LeetCode-307 等